関連状況の記述からの予測
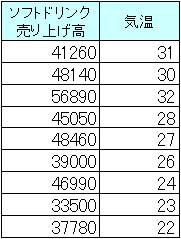 |
| ソフトドリンクと気温の関係 |
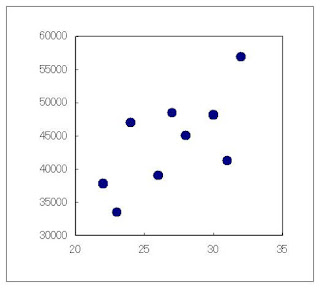
気温とソフトドリンクの売上げ表を見ると、
- 気温の高い日はソフトドリンクの売上が多い
- では、気温が30度位だと、どの程度の売り上げがあるのだろうか?
- 気温が1度上がると、売り上げはどの程度増えるのだろうか?
- 気温から、売上高を予測できないだろうか?
と疑問が湧いてきます。
気温から売り上げを予測するとは?
気温と売り上げを対応させる何らかの関数を与える必要がある
どのような関数(モデル)で予測すれば良いか?
- 曲線を利用した予測
- 階段関数を利用した予測
- 直線を利用した予測 (今回はこれ)
直線の求め方
各データとの距離が一番短くなる直線を選ぶ方法:最上二乗法分析結果
a=1334.2
b=8095.1
よって、
売上高=1334.2×気温+8095.1
気温が1℃上がるたびに、売上が1334.2増えます。
気温が0度の場合は、b=8095.1となります。
 |
| 回帰モデル |
まだ、残差が大きく存在するため、新たな分析モデルを構築する必要性があります。
そして複数の要因で説明する時は、単回帰分析から重回帰分析へと名称が変わる。